§ 9. Географические координаты
Огромное большинство астрономических наблюдений до настоящего времени производится с Земли и зависит от положения наблюдателя на ее поверхности. Поэтому напомним некоторые географические понятия и термины, которыми в дальнейшем мы будем пользоваться.
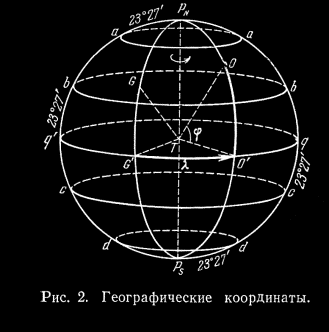
Земля имеет почти шарообразную форму. Воображаемая прямая PN PS , вокруг которой Земля вращается, проходит через центр массы Земли и называется осью вращения (рис. 2).
Ось вращения пересекает поверхность Земли в двух точках: в северном географическом полюсе РN и южном PS. Северный географический полюс тот, со стороны которого вращение Земли происходит против часовой стрелки. Большой круг на поверхности Земли (q' G' O' q), плоскость которого перпендикулярна к оси вращения, называется земным экватором. Он делит поверхность Земли на два полушария: северное (с северным полюсом РN) и южное (с южным полюсом PS).
Малые круги, плоскости которых параллельны плоскости земного экватора, называются географическими параллелями. Географическая параллель (bb), отстоящая на 23° 27' ксеверу от экватора, называется северным тропиком; параллель (cc), отстоящая на 23° 27' к югу от экватора, — южным тропиком. Географические параллели, отстоящие на 23° 27' от полюсов Земли, называются полярными кругами — северным (аа) и южным (dd).
Пояс земной поверхности между тропиками (включая экватор) называется жарким или тропическим поясом. Пояс между северным тропиком и северным полярным кругом называется северным умеренным поясом, а между южным тропиком и южным полярным кругом — южным умеренным поясом. Области земной поверхности за полярными кругами называются северным холодным и южным холодным поясами.
Большой полукруг PNOO'PS, проходящий через географические полюсы Земли и через точку О на ее поверхности, называется географическим меридианом точки О. Географический меридиан PNGG'PS, проходящий через Гринвичскую обсерваторию в Англии, считается нулевым или начальным меридианом. Нулевой меридиан и меридиан, отстоящий от нулевого на 180°, делят поверхность Земли на два полушария: восточное и западное.
Прямая линия ТО, по которой направлена сила тяжести в данной точке Земли, называется отвесной или вертикальной линией.Положение точки О на земной поверхности однозначно определяется двумя географическими координатами: географической широтой j и географической долготой l.
Географической широтой j точки О называется угол О’ТО между плоскостью земного экватора и отвесной линией, проходящей через точку О. Географические широты отсчитываются от экватора в пределах от 0° до +90° (северная широта), если точки лежат в северном полушарии Земли, и от 0° до —90° (южная широта), если точки лежат в южном полушарии.
Географической долготой l точки О называется двугранный угол G'TO' между плоскостями начального меридиана и меридиана, проходящего через точку О. В Советском Союзе принято отсчитывать географическую долготу к востоку от начального меридиана, т.е. в сторону вращения Земли, в пределах от 0° до 360° (в градусной мере), или от 0h до 24h (в часовой мере). Географы, как правило, отсчитывают долготу в пределах от 0 до +180° к востоку (восточная долгота) и от 0 до —180° к западу (западная долгота).
При решении многих астрономических задач можно считать, что Земля представляет собой однородный шар радиусом R = 6370 км. В этом случае направление отвесной линии в любой точке земной поверхности проходит через центр Земли и совпадает с ее радиусом, а географические меридианы и экватор будут окружностями одинакового радиуса, равного радиусу Земли. И тогда географическая широта какой-либо точки на Земле может быть измерена дугой меридиана от экватора до данной точки, а географическая долгота — дугой экватора от начального меридиана до меридиана, проходящего через данную точку.
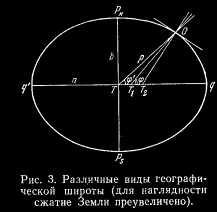
При решении задач, требующих более точных значений размеров и формы Земли, последняя принимается за эллипсоид вращения (сфероид) с неоднородным распределением масс. В этом случае отвесная линия не для всех точек земной поверхности будет проходить через центр сфероида Т (рис. 3), а будет пересекать плоскость земного экватора в некоторой другой точке T1, не совпадая с радиусом-вектором r, т.е. с прямой ТО, соединяющей центр сфероида с точкой О.
Вследствие неравномерного распределения масс в области данной точки отвесная линия Т1O может также не совпадать и с нормалью Т2О к поверхности сфероида, т.е. с перпендикуляром к касательной плоскости в данной точке О Земли. По этому для каждой точки на поверхности Земли необходимо различать три вида географической широты: астрономическую, геоцентрическую и геодезическую.
Астрономической широтой j называется угол O T1 q между плоскостью земного экватора и отвесной линией в данной точке.
Геоцентрической широтой j’ называется угол OTq между плоскостью земного экватора и радиусом-вектором данной точки О.
Геодезической широтой (обозначения не имеет) называется угол O T2 q между плоскостью земного экватора и нормалью к сфероиду в данной точке.
Непосредственно из астрономических наблюдений определяется только астрономическая широта j. Из геодезических и гравиметрических измерений определяется уклонение отвеса в данной точке, т.е. несовпадение отвесной линии с нормалью, которое дает возможность из астрономической широты j получить геодезическую. Уклонение отвеса, как правило, меньше 3" (исключая аномальные места), и в астрономических задачах ими пренебрегают и не делают различия между астрономической и геодезической широтой. Геоцентрическая широта j' вычисляется по формулам аналитической геометрии, связывающим ее с астрономической (точнее, геодезической) широтой. Разность между геоцентрической и астрономической широтой не превышает 12'; на географических полюсах и на экваторе Земли она равна нулю.
|