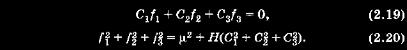2.5. Шестой интеграл уравнений невозмущенного движения
Если провести формальный подсчет полученных интегралов, то насчитаем их семь и, соответственно, семь постоянных: C1 C2 C3 H f1 f2 f3.Однако они не могут составить решения системы уравнений (2.4), так как: а) ни один из них не содержит явно времени; б) имеют место два тождественных соотношения
Соотношение (2.19) может быть легко получено, если левые части интегралов площадей (2.7), (2.8) и (2.9) умножить на левые части интегралов Лапласа (2.17) и полученные результаты сложить. Соотношение (2.19) определяет условие перпендикулярности вектора площадей и вектора Лапласа.
Соотношение (2.20) получают более сложным путем, оно не имеет такой четкой физической интерпретации, как (2.19). Но из него следует важное условие: вектор площадей и вектор Лапласа никогда не могут быть равны нулю одновременно.
Итак, используя соотношения (2.19) и (2.20), можно выразить любые две из семи постоянных в функции пяти остальных, ко-
Соотношения (2.23) и (2.24) дают общий интеграл системы уравнений движения (2.4), так как представляют собой шесть соот пошеннй между временем, пеизвестпыми фупкциями независимыми произвольными постоянными. Более того, (2.23 и (2.24) дают явные выражения для неизвестных величин в за висимости от времени и требуемого числа постоянных.
Следовательно, они представляют собой общее решение сис темы уравнений (2.4). При этом уравнения (2.23) есть параметрические уравнения траектории движущегося КА. Они позволяют определить координаты КА для любого момента времени. Траекторию, по которой движется КА относительно притягивающего тела, называют орбитой (от лат. orbita — колея, путь).
Соотношения (2.24) определяют составляющие скорости КА для любого момента времени, величину модуля скорости
|