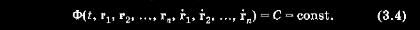3.2. Задача n тел и методы ее решения
В общей постановке определение траектории движения КА с учетом действия сил тяготения Солнца, Земли, планеты-цели (в случае пертурбационного маневра — также и промежуточной планеты) является результатом решения так называемой задачи нескольких тел или задачи n тел, где n — количество взаимо-притягивающих гравитирующих тел. Эта задача не имеет точного математического решения. Небесная механика позволяет решать эту общую задачу различными методами, в том числе и методом решения задачи в упрощенной постановке. Такой задачей, в частности, является задача трех тел, используемая для расчета межпланетных траекторий КА и имеющая в некоторых случаях точное аналитическое решение.
Рассмотрим задачу n тел. Пусть в пространстве выбрана некоторая инерциальная система отсчета, относительно которой в начальный момент времени известны координаты и составляющие скорости п гравитирующих тел. В силу большого расстояния между гравитирующими телами, существенно превышающими их размеры, считают, что масса каждого из тел сосредоточена в его центре тяжести. В дальнейшем для удобства изложения вместо термина «гравитирующее тело» будем употреблять более привычный термин «материальная точка», широко используемый в математике и механике при исследовании различных динамических систем. Из числа сил, действующих на рассматриваемые материальные точки, ограничимся рассмотрением только сил их взаимного притяжения. В результате решения задачи требуется определить координаты каждой из материальных точек системы в любой требуемый момент времени t.
Определение координат любого КА связано с решением соответствующих уравнений движения. При этом метод решения определяется главным образом видом правых частей дифференциальных уравнений. Очевидно, что движение системы л материальных точек описывается системой п векторных дифференциальных уравнений второго порядка:
При днижении системы n материальных точек будет иметь место изменение положения этих точек и их скоростей. Из системы уравнений (3.1) можно найти такие функции координат и скоростей, которые будут оставаться неизменными (инвариантными) в течение всего времени движения:
Для полного решения исследуемой задачи необходимо определить 6n интегралов, поскольку состояние каждой из га точек определяется в инерциальной системе шестью так называемыми фазовыми координатами. Из требуемых 6га интегралов десять первых интегралов системы известны (они получены более двухсот лет назад). Ни одного нового первого интеграла, не являющегося логическим следствием известных, пока не удалось получить. Согласно теории дифференциальных уравнений нахождение каждого нового первого интеграла (в скалярной форме) позволяет понизить порядок системы на единицу. В результате знание десяти первых интегралов позволяет свести задачу к системе (6га - 10) порядка, а знание особенностей структуры самих уравнений (наличие двух квадратур) — понизить порядок системы до (6n - 12). Отсюда можно заключить, какой важный физический смысл имеют указанные известные первые интегралы, получаемые из (3.1) и являющиеся следствием фундаментальных законов теоретической механики: закона сохранения количества движения, закона сохранения момента количества движения и закона сохранения энергии. Действительно, суммируя все уравнения вида (3.1), можно записать
Существующие приближенные методы анализа возмущений, используемые при решении задачи нескольких тел (п > 2), разделяют на класс методов общих (или абсолютных) возмущений и класс методов особых возмущений. Первый класс методов основывают, как правило, на использовании степенных разложений для представления координат каждой из рассматриваемых материальных точек. Второй класс методов предполагает использование приема разделения движения тела на конечное число отрезков (кратное числу гравитирующих тел). В этом случае интегрирование уравнений движения на каждом из этих отрезков осуществляют численным методом и считают, что движение тела в течение короткого интервала времени является вевозмущенным (при известных на заданный момент координатах и скорости тела).
Последний класс методов получил наиболее широкое распространение в механике космического полета. Он включает в себя: метод вариаций элементов, развитый Лагранжем и называемый также методом оскулирующих элементов; метод вариаций координат (со всеми его разновидностями).
Накопленный опыт применения указанных методов для ре-щения разнообразных задач теории космического полета дает основание сформулировать некоторые положения предпочтительного применения того или иного метода.
Метод оскулирующих элементов наиболее приспособлен для решения задач возмущенного движения для не слишком больших интервалов времени исследуемого движения при относительно малых значениях возмущающих сил. Методу вариаций координат отдают предпочтение в случае, когда необходимо произвести вычисление возмущений для длительных промежутков времени при действующих возмущениях, соизмеримых с величиной центральной силы. Применение его целесообразно также для расчета особых возмущений.
Наиболее типичными вариантами алгоритмической реализации данного метода являются: метод Коуэлла (метод непосредственного интегрирования прямоугольных координат); метод Энке, заключающийся в интегрировании отклонений параметров движения КА от опорной (теоретической, номинальной) орбиты.
|