9.3. Показатели точности навигационных определений
Точность навигационных определений зависит от многих факторов. С одной стороны, к ним следует отнести технические особенности организации процесса измерений и обработки полученных данных. Так как в СНС используют искусственно созданные физические поля и радиотехнические принципы приема и передачи информации, то точность навигационных определений сильно зависит от внешних условий и от условий распространения радиоволн. С другой стороны, большое влияние на потенциально достижимую точность навигационных определений оказывает соответствие принятой в НА математической модели реальному физическому процессу.
Неточное знание вероятностных характеристик измеряемых параметров, случайных шумов и возмущений вызывает появление ошибок при решении навигационных задач.
алгоритмические ошибки определения навигационных параметров условно разбивают на две группы. К первой группе относят ошибки, связанные с недостатками, присущими самим алгоритмам. Например, линеаризация исходных нелинейных соотношений приводит к отличию линейной динамической модели, принятой в НА, от реального физического процесса.
Ко второй группе ошибок следует отнести ошибки, связанные в первую очередь с реализацией процесса вычислений в БЦВМ (ошибки округления, потеря точности при делении, ошибки, вызванные конечным значением шага интегрирования ит. д.).
Структурное несовершенство в построении сети СНС приводит к ошибкам, обусловленным невозможностью использования в полном объеме достоинств конкретного метода навигационных определений. Так, например, при дальномерном (дальномерно-разностном) способе определения пространственных координат объекта оптимальное число одновременно наблюдаемых ИСЗ, как было установлено, равно четырем. Отсутствие хотя бы одного ИСЗ в рабочем созвездии вызывает необходимость либо коррекции НА (переход на неоптимальное рабочее созвездие), что связано с изменением вычислительной процедуры и потерей точности, либо с изменением времени сеанса, приводящим, как правило, к ошибкам в определении прогнозируемых значений эфемерид ИСЗ, что также сказывается на точности решения навигационной задачи.
Показателями точности навигационных определений в случае линейной модели движения объекта и нормального распределения вероятностей прежде всего являются математические ожидания определяемых параметров (М[ ♦ ]) и корреляционная матрица P(f), описывающая апостериорную (на момент i-гo измерения) плотность вероятностей навигационных параметров по поступающим измерениям, которая характеризует степень знания вектора состояния объекта после обработки измерений. На практике большая часть математических моделей динамических систем и каналов измерений являются нелинейными, а случайные величины распределены не по нормальному закону. В такой постановке показатели точности носят относительный характер, их определяют приближенно.
связано с изменением вычислительной процедуры и потерей точности, либо с изменением времени сеанса, приводящим, как правило, к ошибкам в определении прогнозируемых значений эфемерид ИСЗ, что также сказывается на точности решения навигационной задачи.
Показателями точности навигационных определений в случае линейной модели движения объекта и нормального распределения вероятностей прежде всего являются математические ожидания определяемых параметров (М[ ♦ ]) и корреляционная матрица P(f), описывающая апостериорную (на момент i-гo измерения) плотность вероятностей навигационных параметров по поступающим измерениям, которая характеризует степень знания вектора состояния объекта после обработки измерений. На практике большая часть математических моделей динамических систем и каналов измерений являются нелинейными, а случайные величины распределены не по нормальному закону. В такой постановке показатели точности носят относительный характер, их определяют приближенно.
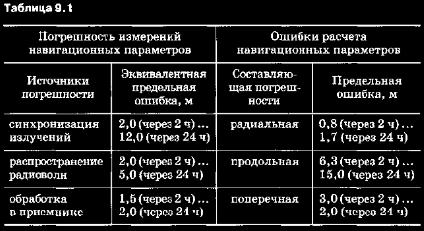
Рассмотрим более подробно характеристики точности СНС. Для системы «Навстар» в [93] приведены экспериментальные данные по погрешностям измерений и предельным ошибкам расчета навигационных параметров (табл. 9.1), на базе анализа которых может быть принята обоснованная зависимость изменения коэффициентов корреляционной матрицы. Так, например, элементы корреляционной матрицы pijt) зависят от взаимного расположения навигационного сигнала и приемной антенны. Однако при соответствующем выборе форм диаграммы направленности приемных и передающих антенн этим обстоятельством можно пренебречь и считать, что вероятностные характеристнки измерений практически не зависят от воаимного положения ИСЗ и определяющегося объекта. Это предположение позволяет существенно упростить процедуру оценки точности решения навигационной задачи. Второе существенное упрощение обусловлено предположением о том, что погрешности расчета навигационных параметров связаны в основном с точностью знания эфемерид ИСЗ. Если погрешности эфемерид невелики, то корреляционная матрица находится через корреляционную матрицу погрешности эфемерид с учетом ошибок прогноза. Однако на практике искомая корреляционная матрица, характеризующая точность навигационных определений, зависит от взаимного положения ИСЗ и определяющегося объекта.
Большое внимание на потенциальную точность при дальномерных методах навигационных определений оказывает относительное положение ИСЗ и объекта. На рис. 9.5 хорошо видно появление узкой нерабочей зоны вблизи трассы ИСЗ, а также постепенное нарастание ошибки при удалении от трассы. Оптимальное удаление при дальномерном способе определений по одному ИСЗ около 500 км. При смещении середины сеанса относительно момента кульминации, т. е. момента прохождения ИСЗ на кратчайшем (траверзном) расстоянии от объекта, усматривают значительное ухудшение точности на «восходе» и «заходе» ИСЗ. При доплеровских (квазидоплеровских) измерениях для тех же самых характеристик сеанса [N и Д() точность определений значительно выше. Ошибка существенно зависит от траверзного расстояния.
Еще большее значение ГФ приобретает при навигационных определениях по созвездию ИСЗ. С точки зрения анализа точности определений принято выделять ЭЛЕМЕНТАРНОЕ СОЗВЕЗДИЕ, ПОД КОТОРЫМ понимают минимальное число ИСЗ, необходимое для определения навигационных параметров. Состав элементарного созвездия зависит как от количества определяемых параметров движения, так и от вида измеряемого навигационного параметра. Например, для определения места (широты и долготы) корабля элементарное созвездие образуют два ИСЗ. В табл. 9.2 приведен [93] состав элементарных созвездий (число ИСЗ) при поверхностном и пространственном определении координат объекта различными способами.
На точность определений существенным образом влияет расположение ИСЗ в созвездии относительно объекта. Например, для элементарного созвездия, состоящего из двух ИСЗ, точность определений будет минимальная при нахождении объекта и спутников в одной плоскости, проходящей через центр Земли. Оптимальным рабочим созвездием из четырех ИСЗ является такое их расположение, при котором образуется тетраэдр максимального объема. При этом, что уже отмечалось, один из ИСЗ находится в зените, а остальные — как можно ближе к горизонту в пределах видимости [93].
Для планирования навигационного обеспечения в различных районах Земли необходимо располагать картами линий равной точности, на которые наносят линии равных ГФ. Эти линии наиболее полно характеризуют зону действия СНС и показывают относительное расположение районов, где точность определений будет не хуже некоторой заданной величины.
Если рассматривать глобальную СНС, охватывающую все районы Земли, то в каждой точке пространства можно определить потенциальную точность навигационного определения. Совокупность таких точек дает возможность построить поле точностей снс.
Нахождение математической модели такого поля является сложной, но весьма актуальной задачей. Трудности построения точностной модели СНС усугубляются еще и тем, что поле точности меняется во времени из-за движении ИСЗ относительно поверхности Земли. Расчеты показывают, что зоны повышенной и пониженной точности совпадают с зонами наибольшего сгущения и наибольшего разрежения ИСЗ. Но не только количество видимых ИСЗ определяет зону наивысшей точности. Как уже отмечалось выше, значительное влияние на точность оказывает и конфигурация выбранного созвездия. Так, минимальная точность достигается в тех зонах, в которых в данный момент реализуется компланарное расположение ИСЗ. Каждый ИСЗ обслуживает в данный момент времени ограниченную область, определяемую зоной его радиовидимости. На границе этой области меняется и точность навигационных определений. Поэтому модель точностного поля или функция точности имеет разрывы второго рода па границе области и первого рода в точках, где наблюдаемые ИСЗ компланарны. Из-за движения ИСЗ границы областей изменяются и конфигурация поля также переменна. Если структура ИСЗ регулярна, т. е. повторяется через определенный промежуток времени, то в поле точности может быть выделена элементарная структура (зона), которая повторяется во времени и в пространстве. Это обстоятельство облегчает построение поля точности СНС.
Для системы GPS, например, размеры такой области составляют 1,5 ч по времени и 60° по долготе. Из-за центральной симметрии СНС в любой момент времени достаточно рассматривать ее точностные свойства только в одном полушарии. В [93] приведены данные о погрешностях определения координат места CIIC типа «Навстар» при обработке измерений от 5 и более ИСЗ в системе с 8-часовым периодом обращения ИСЗ, а также в системе с 12-часовым периодом обращения. Известно, что среднеквадратичные отклонения (СКО) определения места объекта составляют соответственно 6...7ми 7...25м, а высоты — 10... 25 м и 10...45 м. В случае наихудшего расположения рабочего созвездия СКО возрастают по месту до 100... 1000 м и по высоте до 130 м.
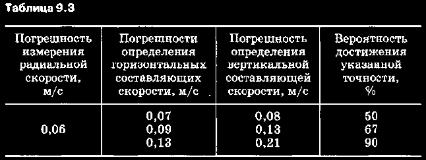
Влияние взаимного расположения ИСЗ в созвездии на погрешности определения скорости потребителя полностью аналогично рассмотренным выше соотношениям для координат. Таким образом, все выводы относительно поля точности для определения координат объекта остаются в силе и для определения скоростей. Порядок погрешностей определения скоростей можно проиллюстрировать данными для системы «Навстар», приведенными в табл. 9.3.
|