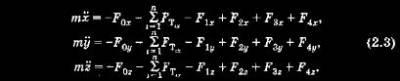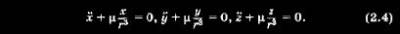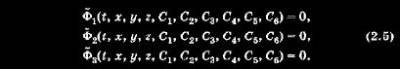Баллистика и навигация космических аппаратов
|
2.1. Математическая модель невозмущенного движения КА Рассматривая абсолютное»движение КА, запишем, используя второй закон Ньютона, дифференциальное уравнение движения в векторной форме в виде При движении около Земли в общем случае следует учитывать еще две силы. Это сила F2 вызванная нецентральностью сил тяготения Земли (прежде всего из-за несферичности и неравномерной плотности Земли), а также аэродинамическая сила F2, возникающая при движении КА в плотных слоях атмосферы. Третий вид сил имеет место в результате работы двигательной установки — это сила тяги F3. Кроме того, в некоторых случаях могут возникать всякого рода дополнительные силы, возникающие, например, в результате травления какого-либо газа из отсеков КА и т. п. Обозначим их через F4. Тогда 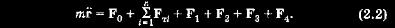 Более наглядный и физически понятный смысл уравнения движения и результаты их решения приобретают при рассмотрении их не в векторном виде, а в проекциях на оси некоторой системы координат, выбор которой занимает важное место при изучении движения КА. В каждом конкретном случае предпочтение отдается той системе, которая дает наглядные результаты, наиболее полно отражающие истинную картину движения. Именно этим определяется огромное число используемых систем координат. При изучении движения ИСЗ широко используют две прямоугольные системы координат, привязанные к центру Земли: ► геоцентрическая инерциальная система координат: начало системы — в центре Земли; основная плоскость OXY — плоскость земного экватора; ось ОХ направлена в точку весеннего равноденствия — это направление Земля — Солнце в день 22 марта (направление на созвездие Овна); ось OZ направлена в полюс Мира (практически совпадает с осью вращения Земли); ось OY дополняет систему до правой; ► гринвичская система координат отличается от геоцентрической инерциальной тем, что ось ОХ лежит в плоскости гринвичского меридиана и направлена по линии пересечения гринвичского меридиана с плоскостью земного экватора. В результате эти системы связаны между собой через угловую скорость вращения Земли 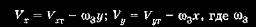 — угловая скорость вращения Земли. При межпланетных полетах в пределах Солнечной системы столь же широко применяют прямоугольные системы, но с началом либо в центре Солнца, либо в центре масс Солнечной системы (барицентр): ► прямоугольная геоэкваториальная система, фиксированная . на заданную эпоху (J2000): начало координат в центре Солнца; основная плоскость OXY — плоскость земного экватора; ось ОХ лежит в плоскости земного экватора и направлена в точку весеннего равноденствия в фиксированную эпоху (время), для J2000 — это 121. 1 января 2000 г., что соответствует юлианской дате JD 245 1545.0; ось OZ направлена в полюс Мира; ► прямоугольная эклиптическая система координат отличается от геоэкваториальной тем, что основной плоскостью OXY является плоскость эклиптики. Перепишем векторное уравнение движения КА (2.2) в проекциях на оси геоцентрической инерциальной системы координат: Знак «минус» в приведенной системе указывает на то, что силы тяготения действуют на КА со стороны Земли и планет. Система дифференциальных уравнений (2.3) имеет шестой порядок и является общей системой уравнений движения естественных и искусственных космических тел, в том числе и ИСЗ. Рассмотрим пассивное движение КА (тяга двигателя F3 = 0). В этом случае основной силой, формирующей движение КА вне плотных слоев атмосферы, является сила тяготения Земли F0; другие силы по величине на несколько порядков меньше F0 и в первом приближении ими можно пренебречь. Составляющими силы F0 являются 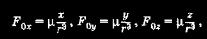 где 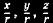 — направляющие косинусы. В результате получим систему уравнений невозмущенного движения ка — направляющие косинусы. В результате получим систему уравнений невозмущенного движения каИтак, невозмущенным называют движение КА, происходящее под действием только центральной составляющей сил тяготения основного притягивающего тела. В поиске решения системы уравнений (2.4) и состоит сущность теории невозмущенного (кеплерова) движения КА. Так как (2.4) является системой 6-го порядка, то для ее решения необходимо определить шесть интегралов. Обшим интегралом системы (2.4) являются соотношения между временем t, координатами КА х, у, г и шестью произвольными постоянными С1, С2,..., С6: Дифференцируя каждое из приведенных уравнений по времени, получим первые интегралы уравнений движения: Таким образом, зная начальные условия движения КА, можно определить произвольные постоянные. Приступим к решению системы уравнений невозмущенного движения (2.4). |
Статьи:
Видео:
Последние новости:
| Человечество спасется за пределами Солнечной системы |
| Комета Хейла-Боппа над перевалом Вал Парола |
| Гималайский горизонт из космоса |
| Звёздная эволюция |
| Солнечная система в объективе веб-камеры |
Видео:
 | SOFIA Flight Tests for Early Science Progress |
 | НЛО. Факты и фальсификации - Наука непознанного |
 | Spacecraft Image Mashup Shows Galactic Collision |
Последние новости:
| Зонд НАСА рассмотрел ледяные горы на поверхности Плутона |
| На Землю надвигается сильный метеоритный дождь |
| NASA создаст роботов для ремонта и дозаправки спутников |
| Россия и Япония совместно построят космический телескоп |
|
WalkInSpace.Ru Правила: «Путешествие в космос» © 2025 Использование материалов допускается при условии указания авторства WalkInSpace.ru и активной ссылки на www.WalkInSpace.ru. |
|