Баллистика и навигация космических аппаратов
|
8.5. Общая постановка задачи баллистического проектирования орбитальных структур СС В отличие от рассмотренной выше упрощенной методики определения структуры орбитальной группировки геометрическим методом, гарантирующей, в лучшем случае, получение решения первого приближения, решение задачи баллистического проектирования позволяет увязать в рамках, единой логической схемы такие процедуры, как определение динамической устойчивости СС на заданном временном интервале ее функционирования, стратегии (закона) управления орбитальными параметрами космического сегмента системы, выбор варианта восполнения его структуры в случае выхода из строя (отказа) одного или нескольких ИСЗ и др.  При подобной достаточно общей постановке решение задачи баллистического проектирования СНС требует огромных затрат машинного времени при проведении расчетов на ЭЦВМ, связанных с определением функции I для всех рабочих зон на всех возможных интервалах функционирования систем in. Более того, решение задачи выбора оптимального варианта построения орбитальной структуры СНС с точки зрения обеспечения точности определения навигационных параметров потенциальных потребителей вообще делает проблематичной возможность получения решения методами численной оптимизации. Это связано с тем, что, во-первых, для однократного вычисления оптимизируемой функции необходимо усреднение значений искомых параметров, характеризующих орбитальное построение СНС, приблизительно в 105 точках временной и географической сетки; во-вторых, оптимизации должна производиться по числу данных параметров, исчисляемых десятками; в-третьих, оптимизируемая функция в этом случае будет иметь большое число локальных экстремумов, нахождение среди которых глобального — пока еще неразрешимая проблема. В этой ситуации в принципе возможны два направления поиска решения. Подчеркнем, что оба они позволяют получить только приближенное решение, однако в данном случае речь идет о приближении иного, более высокого, уровня, чем гарантирует геометрический подход. Первый путь базируется на декомпозиции поставленной задачи и ее частичном упрощении. Прежде всего можно попытаться свести задачу синтеза к выбору такой начальной орбитальной структуры, при которой обеспечивается баллистическая устойчивость СС. В свою очередь, процесс выбора начальной орбитальной структуры, удовлетворяющей условиям баллистической устойчивости, разбивают на несколько этапов, в том числе и на использование геометрического подхода, с последующим примеиением итерационной процедуры поиска последовательных приближений. К числу основных этапов [81] в этом случае относят: ► выбор класса орбит, позволяющих решать задачи, стоящие перед спутниковой системой; ► определение орбитальной структуры начального приближения на основе кинематических соотношений и характерис-► исследование эволюции структуры СС и анализ динамики ее движений; ► уточняющий синтез структуры с учетом орбитальной эволюции и ее влияния на динамику системы. Выделение некоторых частных компонентов из общей задачи баллистического проектирования приводит к отчасти самостоятельному разделу исполнительной баллистики, называемому (81] операционным проектированием. Операционное проектирование по сути представляет собой процесс баллистического сопровождения функционирования СС, в определенной степени адекватный реальным условиям космического полета. 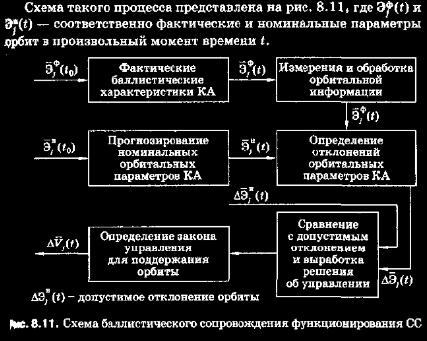 Из схемы следует, что баллистическое сопровождение поле-га ИСЗ СС требует проведения измерений и их обработки, прогнозирования орбитальных параметров, решения текущих задач по определению управляющих параметров для поддержания орбитальных характеристик функционирующей системы пригодными для решения целевых задач. Универсальных методик, решающих задачи операционного проектирования, также не существует. Обычно используют [73] подход, основанный на получении частных решений и их последующей увязке.Вначале предполагают, что стратегия управления выбрана и закон управления фиксирован. При этих предположениях решают задачу выбора начальной орбитальной структуры, обеспечивающей выполнение целевых задач. Затем предполагают, что орбитальное построение СС фиксировано, и определяют закон управления, после чего осуществляют увязку двух частных решений. Второй путь поиска приемлемого варианта орбитальной структуры СС с учетом решаемых ею целевых задач связан с анализом возможных точностных характеристик варьируемых вариантов ее построения с использованием комплексов имитационного моделирования. Данный путь, естественно, является еще более трудоемким и менее формализованным с математической точки зрения. Однако его применение позволяет получить наиболее близкие к достоверным результаты, пользующиеся у разработчиков высоким уровнем доверия. В качестве примера выбора оптимального варианта орбитального построения СНС с использованием имитационного моделирования приведем результаты исследований С. Я. Архипен-кова и В. Ф. Семченко, опубликованные в статье с одноименным названием (см: Космонавтика и ракетостроение — М.: ЦНИИмаш, 1997. — Вып. 9. - С. 186—190). Целесообразность включения в учебник этих материалов обусловлена и тем, что они наглядно иллюстрируют упоминавшийся ранее (см. § 8.1) принцип последовательности при развертывании СНС. В качестве сценария развертывания н использования СНС при моделировании выбирают первоначальную демонстрацию ее возможностей при создании части системы для европейского региона и последующее дополнение региональной СНС до глобальной сетевой системы. В качестве альтернативных вариантов орбит размещения НИСЗ рассматривают следующие: ► круговые орбиты, аналогичные орбитам НИСЗ СС ГЛОНАСС, с наклонением i = 64,8° и полусуточным периодом обращения; ► высокоэллиптические орбиты с суточным периодом обращения а высотами перигея h„ ~ 20 000 км и апогея ha ~ 520 000 км; ► круговые геосинхронные наклонные орбиты (ГСНО) с суточным периодом обращения. Подобная региональная СНС из 8 космических аппаратов может быть расширена до квазиоптимальной глобальной системы, так как в полном составе является частью ее структуры. В заключение приведем результаты сопоставительного анализа основных системных баллистических характеристик действующих СРНС ГЛОНАСС и GPS, полученных первоначально на основе имитационного моделирования и уточненных в процессе функционирования систем (табл. 8.5). Как следует из табл. 8.5, НИСЗ ГЛОНАСС размещают на трех практически круговых орбитах, номинальное значение высот которых составляет 19 100 км (реальное в диапазоне 18 840...19 440 км). Орбитальные плоскости разнесены по долготе восходящего узла на 120°. При полном созвездии НИСЗ в каждой орбитальной плоскости должны равномерно размещаться по 8 спутников с номинальным сдвигом по аргументу широты, равным 45°. Спутники в соседних орбитальных плоскостях сдвинуты на 15° по аргументу широты. Нумерацию орбитальных плоскостей обычно производят по направлению вращения Земли, а нумерацию рабочих (орбитальных) точек — в соответствии с последовательностью расположения НИСЗ на орбите на фиксированный момент времени — против движения. Интервал повторяемости трасс НИСЗ, а следовательно, и зон радиовидимости спутников наземными потребителями составляет 17 витков. Следовательно, НИСЗ СРНС ГЛОНАСС вне попадают» в резонанс с вращением Земли, совершая указанное количество обращений (семнадцать) примерно за 8 сут, а точнее за 7 сут 23 ч 27 мин 28 с. При этом начало каждого витка смещается относительно поверхности Земли приблизительно на 21° по долготе. В результате достигается высокий уровень стабильности группировки, превосходящей уровень стабильности СРНС GPS с синхронными 12-часовыми орбитами. К тому же доступность НИСЗ в СРНС ГЛОНАСС на широтах более 50° выше, чем в системе GPS. Последнее обусловлено большим значением угла наклонения обит спутников СРНС ГЛОНАСС.  |
Статьи:
Видео:
Последние новости:
| Кратер Галле - смайлик :) |
| Долгое лунное затмение |
| Лучшие 30 снимков АМС «Кассини» |
| Молодая звезда, темное облако |
| Орбитальный самолет Boeing X-37B |
Видео:
 | Spacecraft Image Mashup Shows Galactic Collision |
 | Hubble Unveils Never-Before-Seen Galaxies |
 | Устройство НЛО, чертёж |
Последние новости:
| Зонд НАСА рассмотрел ледяные горы на поверхности Плутона |
| На Землю надвигается сильный метеоритный дождь |
| NASA создаст роботов для ремонта и дозаправки спутников |
| Россия и Япония совместно построят космический телескоп |
|
WalkInSpace.Ru Правила: «Путешествие в космос» © 2025 Использование материалов допускается при условии указания авторства WalkInSpace.ru и активной ссылки на www.WalkInSpace.ru. |
|



