16.7. Оптимальное управление на участке основного аэродинамического торможения
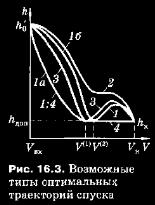
Сформулируем задачу оптимального управления на участке основного аэродинамического торможения для случая использования реактивной СМП. На участке основного аэродинамического торможения требуется определить программу управления эффективным аэродинамическим качеством из условия обеспечения минимума конечной скорости при ограничении на управление и на высоту полета и при заданных конечных значениях параметров траектории. Решение сформулированной задачи показывает, что в зависимости от начальных условий входа и параметров К А возможны четыре типа оптимальных траекторий спуска (рис. 16.3):
► оптимальная траектория содержит участки выхода, движения по ограничению и последующего схода с ограничения внутрь допустимой области фазовых координат (кривая!; 1а, 16 — граничные траектории);
► оптимальная траектория целиком лежит внутри допустимой области фазовых координат (кривая 2);
► оптимальная траектория касается ограничения h = haan (кривая 3);
► оптимальная траектория состоит из двух участков — выхода на ограничение и движения по нему (кривая 4).
При движении внутри допустимой области фазовых координат для любого типа оптимальных траекторий эффективное качество может принимать только граничные значения Кэф = -К6 или Кэф = Къ. Количество переключений Кэф с одного граничного значения на другое определяется конкретными параметрами КА, поставленными ограничениями и начальными условиями входа в атмосферу.
Рассмотрим задачу поиска оптимального управления КА на участке основного аэродинамического торможения в предположении использования парашютно-реактивной СМП. Она сформулирована следующим образом: при заданных начальных условиях, ограничениях на управление и фазовые координаты необходимо определить такой закон управления эффективным качеством, при котором функционал I = hx достигает максимума.
Проведенные исследования показали, что сформулированная задача эквивалентна рассмотренной выше задаче о минимуме конечной скорости спуска и ее решение имеет однотипную структуру оптимального управления.
|